![https://leetcode.com/problems/is-graph-bipartite/]
Given an undirected graph, return true if and only if it is bipartite.
Recall that a graph is bipartite if we can split its set of nodes into two independent subsets A and B, such that every edge in the graph has one node in A and another node in B.
The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice.
1
2
3
4
5
| Example 1:
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can divide the vertices into two groups: {0, 2} and {1, 3}.
|
1
2
3
4
5
| Example 2:
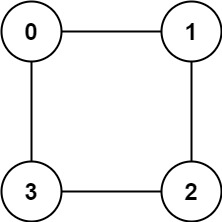
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: We cannot find a way to divide the set of nodes into two independent subsets.
|

Constraints:
- 1 <= graph.length <= 100
- 0 <= graph[i].length < 100
- 0 <= graph[i][j] <= graph.length - 1
- graph[i][j] != i
- All the values of graph[i] are unique.
- The graph is guaranteed to be undirected.
Solution Union Edges in One Component#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| class Solution {
public boolean isBipartite(int[][] graph) {
int n = graph.length;
UF uf = new UF(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j + 1 < graph[i].length; j++) {
// all nodes from graph[i] should be in one component
uf.union(graph[i][j], graph[i][j + 1]);
}
}
/*
[[1,3],[0,2],[1,3],[0,2]]
0123
0
*/
for (int i = 0; i < n; i++) {
for (int j = 0; j < graph[i].length; j++) {
if (uf.find(i) == uf.find(graph[i][j])) {
return false;
}
}
}
return true;
}
public class UF {
private int[] a;
public UF(int n) {
this.a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = i;
}
}
void union(int p, int q) {
int pid = find(p);
int qid = find(q);
a[qid] = pid;
}
int find(int p) {
while (p != a[p]) {
p = a[p];
}
return p;
}
}
}
|
Solution DFS Colouring#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] colors = new int[n];
Arrays.fill(colors, -1);
for (int start = 0; start < n; start++) {
if (colors[start] != -1) continue;
Stack<Integer> stack = new Stack<>();
stack.push(start);
colors[start] = 0;
while (stack.size() > 0) {
int node = stack.pop();
for (int nei: graph[node]) { // 1, 3
if (colors[nei] == -1) {
colors[nei] = colors[node] ^ 1;
stack.push(nei);
} else if (colors[node] == colors[nei]) {
return false;
}
}
}
}
return true;
}
|

