108. Convert Sorted Array to Binary Search Tree

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

ex1

1
2
3
4
5
Example 1:

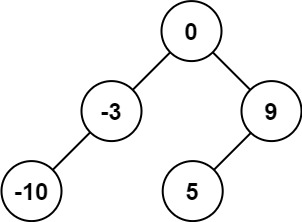
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
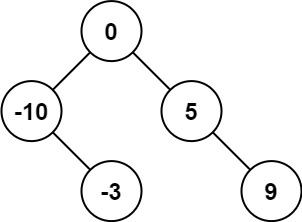
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

ex2

1
2
3
4
5
Example 2:

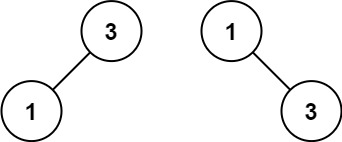
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,3] and [3,1] are both a height-balanced BSTs.

ex3

Constraints:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums is sorted in a strictly increasing order.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) return null;
        return buildBST(nums, 0, nums.length - 1);
    }
    
    TreeNode buildBST(int[] nums, int lo, int hi) {
        if (hi < lo) {
            return null;
        }
        TreeNode node = new TreeNode();
        int mid = lo +  (hi  - lo) / 2;
        node.val = nums[mid];
        node.left = buildBST(nums, lo, mid - 1);
        node.right = buildBST(nums, mid + 1, hi);
        return node;
    }
}