797. All Paths From Source to Target
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1, and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
1
2
3
4
5
| Example 1:
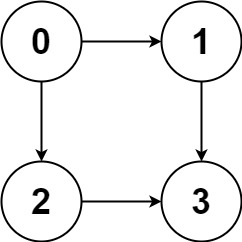
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
|
1
2
3
4
| Example 2:
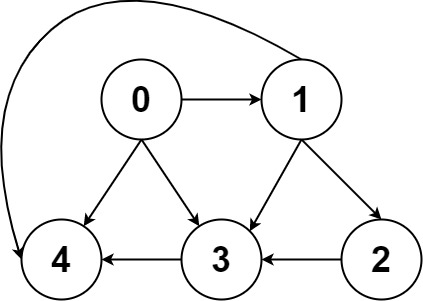
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
|
1
2
3
4
| Example 3:
Input: graph = [[1],[]]
Output: [[0,1]]
|
1
2
3
4
| Example 4:
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]
|
1
2
3
4
| Example 5:
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]
|
Constraints:
- n == graph.length
- 2 <= n <= 15
- 0 <= graph[i][j] < n
- graph[i][j] != i (i.e., there will be no self-loops).
- The input graph is guaranteed to be a DAG.
Solution#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<Integer> paths = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
build(0, graph, paths, res);
return res;
}
void build(int s, int[][] g, List<Integer> paths, List<List<Integer>> res) {
paths.add(s);
if (s == g.length - 1) {
res.add(new ArrayList<>(paths));
} else {
for (int v : g[s]) {
build(v, g, paths, res);
}
}
paths.remove(paths.size() - 1);
}
}
|
Solution 08.05.2021#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int[] visited = new int[graph.length];
dfs(0, graph, visited, path, res);
return res;
}
void dfs(int v,
int[][] graph,
int[] visited, List<Integer> path, List<List<Integer>> res) {
if (visited[v] == 1) return;
visited[v] = 1;
path.add(v);
if (v == graph.length - 1) {
res.add(List.copyOf(path));
}
for (int e: graph[v]) {
dfs(e, graph, visited, path, res);
}
visited[v] = 0;
path.remove(path.size() - 1);
}
}
|
Solution 19.10.2021#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<List<Integer>> paths = new ArrayList<>();
List<Integer> curr = new ArrayList<>();
curr.add(0);
dfs(0, graph.length - 1, graph, curr, paths);
return paths;
}
void dfs(int source, int target, int[][] graph, List<Integer> curr, List<List<Integer>> paths) {
if (source == target) {
paths.add(List.copyOf(curr));
return;
}
for (int dest: graph[source]) {
curr.add(dest);
dfs(dest, target, graph, curr, paths);
Integer last = curr.remove(curr.size() - 1);
}
}
}
|

