563. Binary Tree Tilt

Given the root of a binary tree, return the sum of every tree node’s tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if there the node does not have a right child.

1
2
3
4
5
6
7
8
9
Example 1:

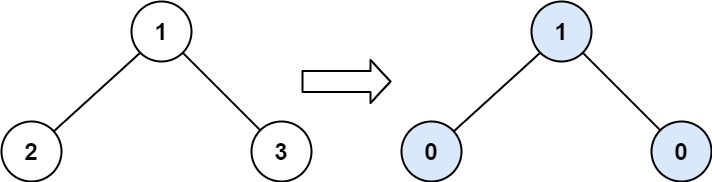
Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

ex1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
Example 2:

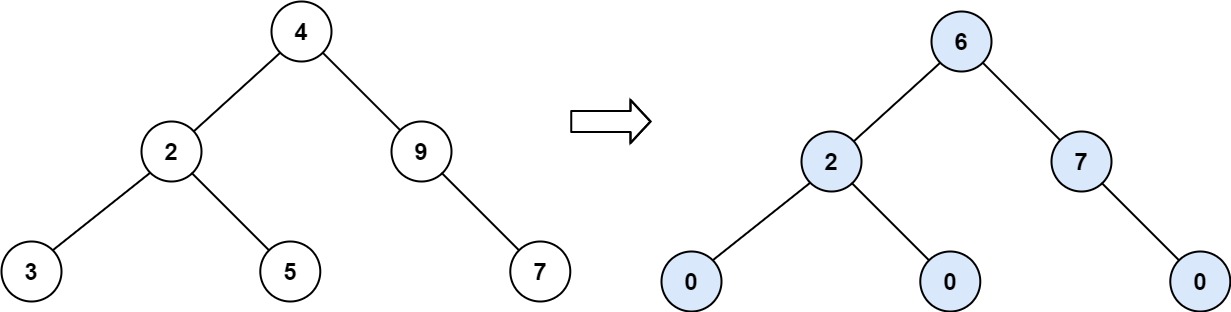
Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

ex2

1
2
3
4
Example 3:

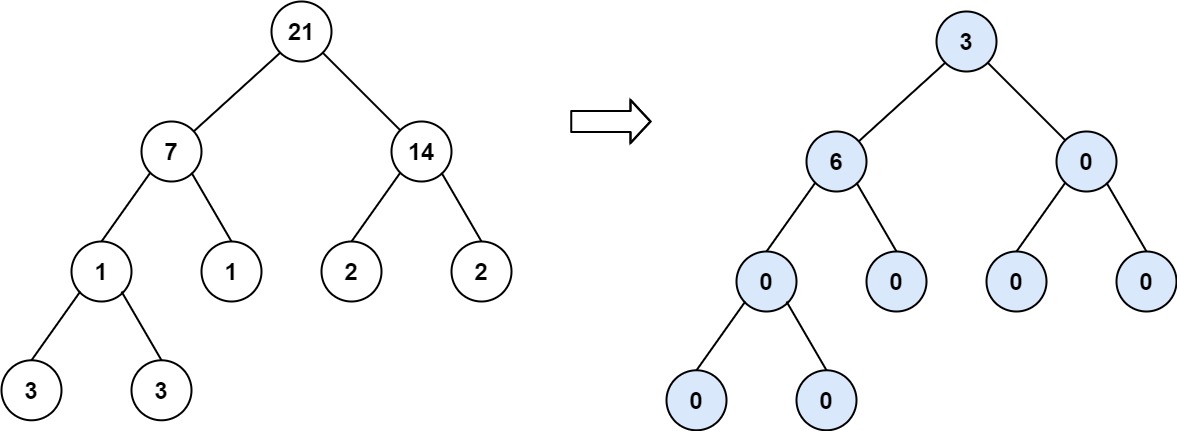
Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

ex3

Constraints:

The number of nodes in the tree is in the range [0, 104].
-1000 <= Node.val <= 1000

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    int[][] dirs = new int [][] {
        {1, 0},
        {-1, 0},
        {0, 1},
        {0, -1}
    };
    public int closedIsland(int[][] grid) {
        int count = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 0 && dfs(i, j, grid)) count++;
            }
        }
        return count;
    }
    
    boolean dfs(int i, int j, int[][] grid) {
        if (i < 0 || i >= grid.length 
           || j < 0 || j >= grid[0].length) {
            return false;
        }
        
        if (grid[i][j] == 1) {
            return true;
        }
        
        grid[i][j] = 1;
        
        boolean closed = true;
        for (int[] dir: dirs) {
            closed = closed & dfs(dir[0] + i, dir[1] + j, grid);
        }
        return closed;
    }
}

Solution#

Solution