1557. Minimum Number of Vertices to Reach All Nodes

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

1
2
3
4
5
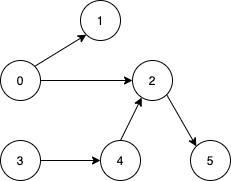
Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

ex1

1
2
3
4
5
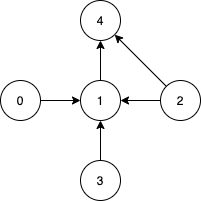
Example 2:

Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

ex2

Constraints:

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi < n
All pairs (fromi, toi) are distinct.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        int[] indegree = new int[n];
        
        for (var e: edges) {
            indegree[e.get(1)]++;
        }
        
        List<Integer> res = new ArrayList<>();
        for (int i = 0; i < indegree.length; i++) {
            int v = indegree[i];
            if (v == 0) {
                res.add(i);
            }
        }
        return res;
    }
}

Solution#

Solution