51. N-Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
Example 1:

Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

ex1

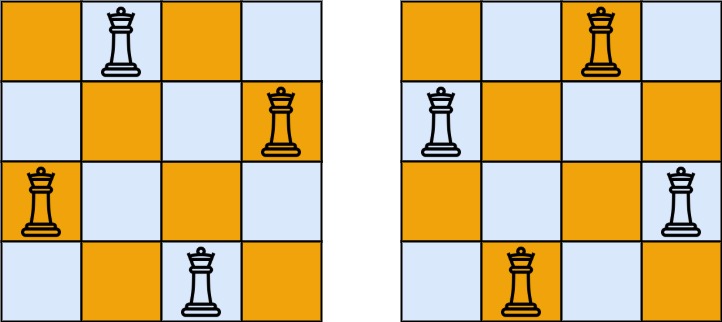
Constraints:

1 <= n <= 9

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
class Solution {

    public List<List<String>> solveNQueens(int n) {
        int[][] board = new int[n][n];
        Set<List<String>> res = new HashSet<>();
        
        backtrack(n, 0, board, res);
        
        return new ArrayList<>(res);
    }
    
    void backtrack(int n, int k,
                  int[][] board, Set<List<String>> res) {
        // System.out.println();
        // for (String line: toList(board)) {
        //     System.out.println(line);
        // }
        
        if (k == n) {
            res.add(toList(board));
            return;
        }
        
        for (int j = 0; j < n; j++) {
             if (canPut(board, k, j)) {
                    board[k][j] = 1;
                    backtrack(n, k + 1, board, res);
                    board[k][j] = 0;   
            }
        }       
    }
    
    boolean canPut(int[][] board, int i, int j) {
        int n = board.length;
        // check rows
        for (int col = 0; col < n; col++) {
            if (board[i][col] == 1) return false;
        }
        
        // check cols
        for (int row = 0; row < n; row++) {
             if (board[row][j] == 1) return false;
        }
        
        /*
        
        00 01 02 03
        10 11 12 13
        20 21 22 23
        30 31 32 33

        */
        for (int row = 0; row < n; row++) {
            for (int col = 0; col < n; col++) {
                 // check first diagonal
                if (i - j == row - col && board[row][col] == 1) {
                    return false;
                }
                
                // check second diagonal
                if (i + j == row + col && board[row][col] == 1) {
                    return false;
                }
            }
         }
        
        return true;
    }
    
    List<String> toList(int[][] board) {
         int n = board.length;
         List<String> res = new ArrayList<>();
         for (int row = 0; row < n; row++) {
            StringBuilder sb = new StringBuilder(); 
            for (int col = 0; col < n; col++) {
                if (board[row][col] == 1) {
                    sb.append("Q");
                } else {
                    sb.append(".");
                }
            }
            res.add(sb.toString()); 
         }
        return res;
    }
}

Solution#

Solution