1123. Lowest Common Ancestor of Deepest Leaves

Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

The node of a binary tree is a leaf if and only if it has no children
The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1.
The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A.

1
2
3
4
5
6
7
Example 1:

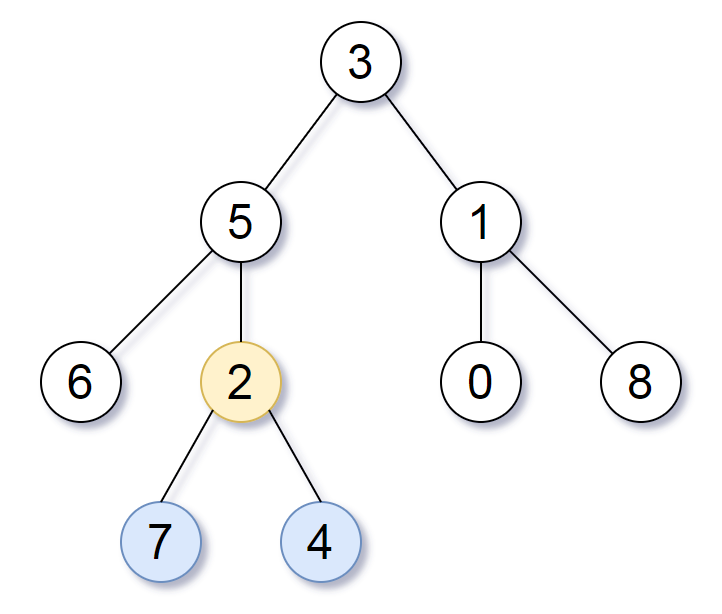
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest leaf-nodes of the tree.
Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

ex1

1
2
3
4
5
Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.

1
2
3
4
5
Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

Constraints:

The number of nodes in the tree will be in the range [1, 1000].
0 <= Node.val <= 1000
The values of the nodes in the tree are unique.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int max = 0;
    TreeNode lca = null;
    public TreeNode lcaDeepestLeaves(TreeNode root) {
        deepest(root, 0);
        return lca;
    }
    
    int deepest(TreeNode node, int level) {
        if (node == null) return 0;
        
        if (level > max) {
            max = level;
            lca = node;
        }
        
        int leftMax = deepest(node.left, level + 1);
        int rightMax = deepest(node.right, level + 1);
    
        
        if (leftMax == max && rightMax == max) {
            lca = node;
        }
        
        return Math.max(level, Math.max(leftMax, rightMax));
    }
}

Solution#

Solution