1382. Balance a Binary Search Tree

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

ex1

1
2
3
4
5
Example 1:

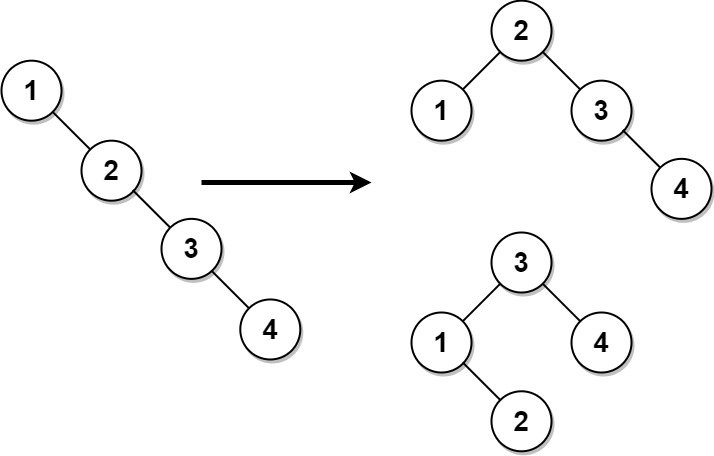
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

ex2

1
2
3
4
Example 2:

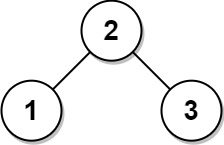
Input: root = [2,1,3]
Output: [2,1,3]

Constraints:

The number of nodes in the tree is in the range [1, 10^4].
1 <= Node.val <= 10^5

Solution Recursive

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode balanceBST(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        
        dfs(root, list);
        
        int n = list.size();
        return buildTree(list, 0, n - 1);
    }
    
    TreeNode buildTree(List<Integer> res, int lo, int hi) {
        
        if (lo > hi) return null;
        
        int mid = lo + (hi - lo) / 2;
        TreeNode node = new TreeNode(res.get(mid));
        node.left = buildTree(res, lo, mid - 1);
        node.right = buildTree(res, mid + 1, hi);
        
        return node;
    }
    
    void dfs(TreeNode node, List<Integer> res) {
        if (node == null) return;
        
        dfs(node.left, res);
        
        res.add(node.val);
        
        dfs(node.right, res);
    }
}

Solution Recursive#

Solution Recursive