Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
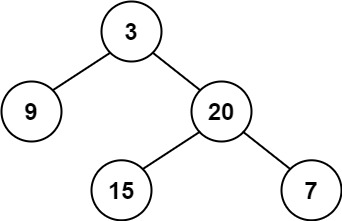
Input: root = [3,9,20,null,null,15,7]
Output: true
Example 2:
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:
Input: root = []
Output: true
Constraints:
- The number of nodes in the tree is in the range [0, 5000].
- -104 <= Node.val <= 104
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length == 0) return null;
return buildBST(nums, 0, nums.length - 1);
}
TreeNode buildBST(int[] nums, int lo, int hi) {
if (hi < lo) {
return null;
}
TreeNode node = new TreeNode();
int mid = lo + (hi - lo) / 2;
node.val = nums[mid];
node.left = buildBST(nums, lo, mid - 1);
node.right = buildBST(nums, mid + 1, hi);
return node;
}
}
Solution 2021-11-08
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
int getHeight(TreeNode node) {
if (node == null) return 0;
int left = getHeight(node.left);
int right = getHeight(node.right);
if (left == -1 || right == -1) return -1;
if (Math.abs(left - right) > 1) {
return -1;
}
return Math.max(left, right) + 1;
}
public boolean isBalancedTopDown(TreeNode root) {
if (root == null) return true;
int left = longest(root.left);
int right = longest(root.right);
return Math.abs(left - right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
int longest(TreeNode node) {
if (node == null) return 0;
return Math.max(longest(node.left), longest(node.right)) + 1;
}
}
Solution 2021-11-20
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
int left = height(root.left);
int right = height(root.right);
// BOTTOM-UP
return isBalanced(root.left) && isBalanced(root.right) && Math.abs(left - right) <= 1;
// TOP-DOWN
// return Math.abs(left - right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
int height(TreeNode node) {
if (node == null) return 0;
return Math.max(height(node.left), height(node.right)) + 1;
}
}