1254. Number of Closed Islands

Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

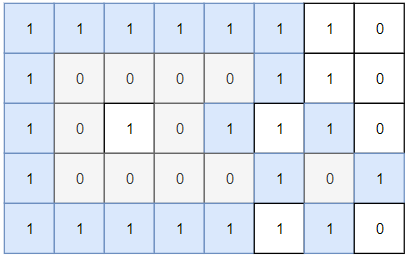
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

ex1

Example 2:

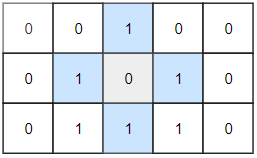
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

ex1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

1 <= grid.length, grid[0].length <= 100
0 <= grid[i][j] <=1

Solution

class Solution {
    int[][] dirs = new int [][] {
        {1, 0},
        {-1, 0},
        {0, 1},
        {0, -1}
    };
    public int closedIsland(int[][] grid) {
        int count = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 0 && dfs(i, j, grid)) count++;
            }
        }
        return count;
    }
    
    boolean dfs(int i, int j, int[][] grid) {
        if (i < 0 || i >= grid.length 
           || j < 0 || j >= grid[0].length) {
            return false;
        }
        
        if (grid[i][j] == 1) {
            return true;
        }
        
        grid[i][j] = 1;
        
        boolean closed = true;
        for (int[] dir: dirs) {
            closed = closed & dfs(dir[0] + i, dir[1] + j, grid);
        }
        return closed;
    }
}

Solution#

Solution