2654. Maximum Binary Tree

654. Maximum Binary Tree

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

Example 1:

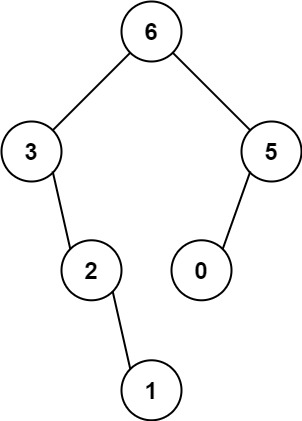
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

ex1

Example 2:

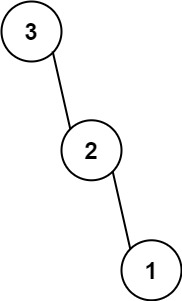
Input: nums = [3,2,1]
Output: [3,null,2,null,1]

ex2

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
        //int this que we need to work seperately on the left side of max element and on the right side of maxElement
        //so we required a data structure that give us this functionality that while going from left to right if there is any max element between left and right then
        //we can separate them
        //here monotonic Stack can help us if we will put element in decreasing order then 
        //if any max element comes then we will pop the element from stack untill stackTop is less than max element and we will make
		//(stack max element) (which is last poped max element)  to the left child of maxelement         
        //if lesser element comes then we will make it right child of stackTOp
    
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        Stack<TreeNode> stack = new Stack<>();
        
        for (int i = 0; i < nums.length; i++) {
            TreeNode curr = new TreeNode(nums[i]);
            
            while (stack.size() > 0 && stack.peek().val < nums[i]) {
                curr.left = stack.pop();
            }
            
            if (stack.size() > 0) {
                stack.peek().right = curr;
            }
            
            stack.push(curr);
        }
        while (stack.size() > 1) stack.pop();
        
        return stack.peek();
    }
}

Solution#

Solution