261. Graph Valid Tree

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

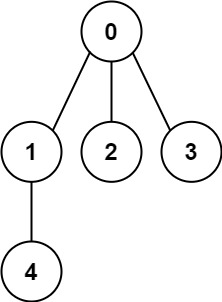
Example 1:

Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

ex1

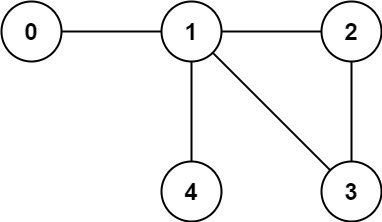
Example 2:

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

ex2

Constraints:

1 <= 2000 <= n
0 <= edges.length <= 5000
edges[i].length == 2
0 <= ai, bi < n
ai != bi
There are no self-loops or repeated edges.

Solution

class Solution {
    public boolean validTree(int n, int[][] edges) {
          Map<Integer, List<Integer>> graph = new HashMap<>();

          for (int i = 0; i < n; i++) {
                graph.put(i, new ArrayList<>());
          }

          for (int[] edge: edges) {
                int source = edge[0];
                int target = edge[1];

              graph.get(source).add(target);
              graph.get(target).add(source);
            }

            // [ {1: 2,3,4}, {2: {5,6}}]

            boolean[] visited = new boolean[n];

            boolean hasCycles = dfs(0, -1, graph, visited);
            if (hasCycles) {
                    return false;
            }        

            for (boolean hasVisit: visited) {
                if (!hasVisit) {
                    return false;
                }
            }    

            return true;
    }
    
    boolean dfs(int start, int prev, Map<Integer, List<Integer>> graph, boolean[] visited) {
    // already visited, has cycle
      if (visited[start]) {
            return true;
      }

        visited[start] = true;

        for (Integer node: graph.get(start)) {

            if (node == prev) continue;

            boolean hasCycle = dfs(node, start, graph, visited);
            
            if (hasCycle) {
                return true;
            }            
        }
        
        return false;
    }
}

Solution#

Solution